Algorithms Analyses
📐 Algorithm complexity
Time complexity
Time complexity specifies how long it will take to execute an algorithm as a function of its input size. It provides an upper-bound on the running time of an algorithm.
Space complexity
Space complexity specifies the total amount of memory required to execute an algorithm as a function of the size of the input.
📈 Order Of Growth
Classifications
| order of growth | name | description | example |
|---|---|---|---|
| 1 | Constant | statement | add two numbers |
| log N | Logarithmic | divide in half | binary search |
| N | Linear | loop | find the maximum |
| N log N | Linearithmic | divide and conquer | mergesort |
| N2 | Quadratic | double loop | check all pairs |
| N3 | Cubic | triple loop | check all triples |
| 2n | Exponential | exhaustive search | check all subsets |
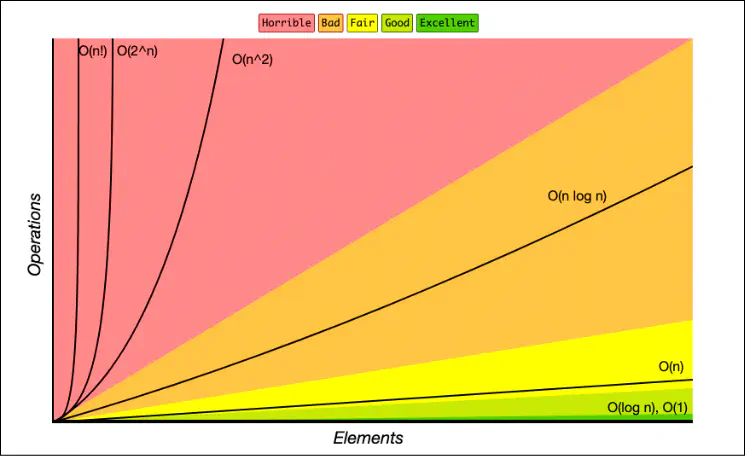
Simplification
- Drop constants. Constants do not affect the algorithm’s growth rate relative to its input.
O(3n2) -> O(n2)
- Lower-Order terms. There is a focus on the dominant term that contributes the most to the growth rate.
O(n2 + 5n + 10) -> O(n2)
- Use Summation for Multiple operations. Multiple operations with a different time complexity can be summed.
O(n) and O(log n) -> O(n + log n) -> O(n) (because of the dominant term)
- Drop Non-Dominant Terms in Additions. We need to leave only the terms that dominate the growth rate.
O(n2 + n) -> O(n2)
- Multiplication rule for Nested arrays.
O(n) loop with a nested O(m) loop -> O(n * m)
- Consider the Worst-Case Scenario. Big O notation focuses on the worst-case scenarios, so it needs to be simplified based on the worst-case analysis.
🔭 Asymptotic Notations
There are mathematical notations used to describe an algorithm’s performance in relation to the amount of input data:
- Big O - worst case (upper-bound on cost)
- Big Ω (Omega) - best case (lower-bound on cost)
- Big Θ (Theta) - average case (“expected” cost)
Big O
Big O notation represents an algorithm’s worst-case complexity. It defines how the performance of the algorithm will change as an input size grows.