Queue

Overview

Similarly to a Stack, a Queue is a linear data structure where the elements are inserted and removed in a specific order. It follows the FIFO (First In, Last Out) principle, where the first added element is the first one to be removed.

Data Structures - Queue

Queue Types

  • Input Restricted Queue. A queue, where the elements can be retrieved only from one end, but deletion can be done from both ends.
  • Output Restricted Queue. A queue, where the elements can be retrieved from both ends, but deletion can be done from only one end.
  • Circular Queue. A queue, where the last position is connected back to the first position.
  • Dequeue (Double-Ended Queue). Insertion and deletion operations can be performed for both ends.
  • Priority Queue. A queue, where the elements are retrieved based on their priority, not the insertion order.

Operations

OperationDescriptionTime Complexity
EnqueueAdd an element to the end of the queueO(1)
DequeueRetrieve and remove an element from the start of the queueO(1)
PeekRetrieve an element from the start of the queue without removing itO(1)

Advantages

  • Queues are used in the implementation of other data structures
  • Queues provide constant time complexity for its core operations

Disadvantages

  • Not suitable for searching accessing its middle elements
  • Limited size on an array implementation
  • Additional space required on a linked list implementation

Use Cases

  • Operating systems (CPU, disk scheduling)
  • Breath-First Search
  • To handle multiple producers by a single consumer

Implementation

Custom Implementation

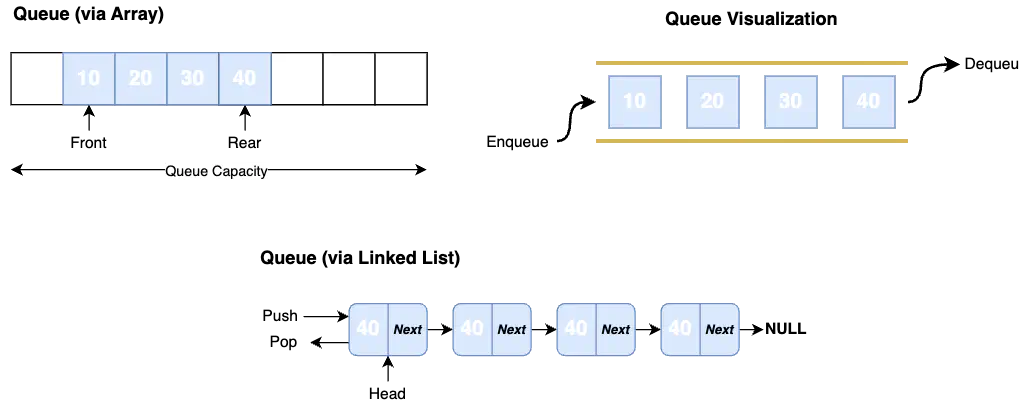
A Queue can be represented as an array or a linked list. In the case of an array, we need to store the indexes of the first and last stored elements. For the linked list, we need to have pointers to the head and tail list nodes.

public class QueueArray<T> {
  private T[] queue;
  private int front = -1; 
  private int rear = -1; 
  
  public QueueArray(int capacity) {
    this.queue = (T[]) new Object[capacity];
  }

  public void enqueue(T value) {
    if (isFull()) return;

    queue[++rear] = value;
    if (front == -1) front++;
  }

  public T dequeue() {
    if (isEmpty()) return null;

    if (front == rear) {
      T value = queue[front];
      front = rear = -1;
      return value;
    }
    return queue[front++];
  }

  public boolean isEmpty() {
    return front == -1 && rear == -1;
  }

  public boolean isFull() {
    return rear >= (queue.length - 1);
  }
}

public class QueueLinkedList<T> {
  private class Node {
    public T value;
    public Node next;
  }

  private Node head;    // "end" of the queue
  private Node tail;    // "start" of the queue

  // Add an element to the start of the queue
  public void enqueue(T value) {
    Node node = new Node();
    node.value = value;

    if (isEmpty()) {
      head = node;
    } else {
      tail.next = node;
    }

    tail = node;
  }

  // Take and remove the element at the end of the queue
  public T dequeue() {
    T value = head.value;

    if (tail == head) tail = head.next;
    head = head.next;

    return value;
  }

  public T peek() {
    return head.value;
  }
}

Built-in Examples 

ArrayDeque<String> queue = new ArrayDeque<>();
    
queue.add("First");
queue.add("Second");
queue.add("Third");

queue.peek();       // "First"
queue.poll();       // "First"
queue.size();       // 2
queue.isEmpty();    // false

LinkedList<String> queue = new LinkedList<>();
    
queue.add("First");
queue.add("Second");
queue.add("Third");

queue.peek();       // "First"
queue.poll();       // "First"
queue.size();       // 2
queue.isEmpty();    // false

const queue: string[] = [];

queue.push("First");
queue.push("Second");
queue.push("Third");

queue[0];           // "First"
queue.shift();      // "First"
queue.length;       // 2      
queue.length === 0; // false

Resources

← Stack
Heap →