Heap

The Heap is a Tree-based data structure where the tree is a complete binary tree. It allows storing duplicates. Despite the Tree-based visualization, Heap is implemented using an array. In many cases, the Heap data structure is also referred to as a Priority Queue.

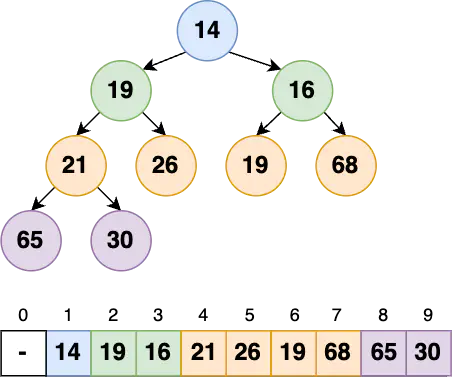
Types #

Max-Heap #

The key of the root node must be the greatest among all of its children. The same rule is applied for all sub-trees.

Min-Heap #

The key of the root node must be the minimal among all of its children. The same rule is applied for all sub-trees.

Operations #

Elements Access #

• Current: heap[i]
• Parent: heap[i / 2]
• Left Child: heap[2 * i]
• Right Child: heap[2 * i + 1]

Peek #

The process of retrieving the top element of the heap without deleting it.

// Time Complexity: O(1)
public T peek() {
  return heap.size() == 1 ? null : heap.get(1);
}

Insertion #

1. Insert a new element to the end of the heap array
2. Compare the element’s node with its parent (i/2)
   • If the parent’s value is larger than the current node’s value (heap[i/2] > heap[i]), we swap them and run step №2 again from the new position
   • If the parent’s value is smaller or equal we exit from the loop

// Time Complexity: O(log N)
public void push(T value) {
  heap.add(value); // add value to the end

  int i = heap.size() - 1;
  while (i > 1 && heap.get(i) < heap.get(i / 2)) {
    // Swap child and parent node values until
    // the parent is less then the inserted value
    swap(i, i / 2);
    i = i / 2;
  }
}

Deletion #

The deletion process of the top element of the heap, and then organizing the heap and returning the deleted element with time complexity O(log N).

1. Extract the top value (heap[1])
2. Put the last node to the top (heap[1] = heap[heap.length - 1])
3. Percolate the top node down until it’s in the right position:
   • Pick a minimum of two children
   • Compare the picked minimum node to the current element
   • If the child is smaller, we swap the nodes

// Time Complexity: O(log N)
public int poll() {
  if (heap.size() == 1) return null; // Heap is empty
  if (heap.size() == 2) return heap.remove(1); // Heap contains 1 element

  int result = heap.get(1); // Get first (root) element 

  // Move the last value to the root
  heap.set(1, heap.remove(heap.size() - 1));

  // Percolate root value down the heap
  int i = 1;
  while (i * 2 < heap.size()) {
    int minIdx = i * 2;
    int rightChildIdx = i * 2 + 1;

    if (rightChildIdx < heap.size() && heap.get(rightChildIdx) < heap.get(minIdx))
      minIdx = rightChildIdx;

    if (heap.get(i) < heap.get(minIdx)) break;

    swap(i, minIdx);
    i = minIdx;
  }
  
  return result;
}

Heapify #

The process of creating a heap from an array.

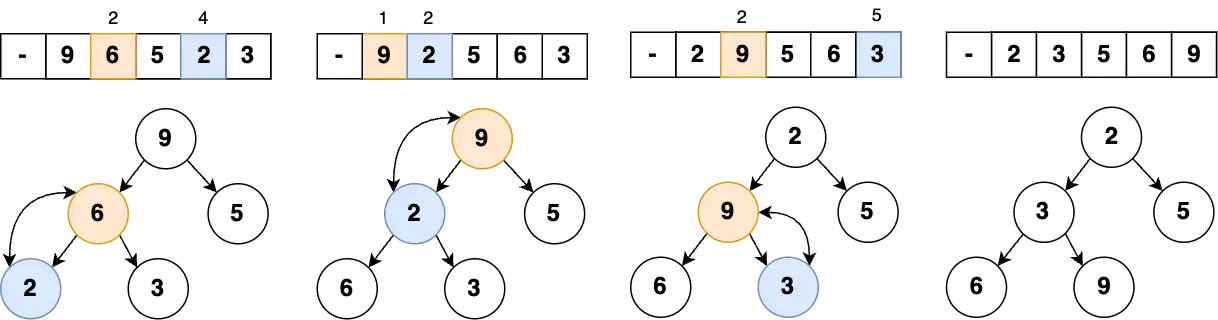
1. Move the 0-index element to the end of the array
2. Go to the half of the array (heap.length / 2)
3. Percolate the node down until it’s in the right position:
   • Pick a minimum of two children (i/2 and i/2+1)
   • Compare the minimum child to the parent
   • If the child is smaller, we swap the node

// Time Complexity: O(N)
private void heapify(int[] items) {
  heap = new ArrayList<>();
  heap.add(null);  // first index element is unused

  // Add all items to the heap
  for (int item : items) heap.add(item);

  // Percolate values down the heap
  for (int i = heap.size() / 2; i >= 1; i--)
    percolateDown(i); // see "poll()" method
}

Usage #

• Priority Queue is commonly implemented using the Heap data structure because it performs its operations in O(log N) time
• Heap Sort algorithm uses the Heap to sort an array in O(N log N) time
• Order statistics problems (to find the Kth smallest/largest element in an array) can be efficiently solved with a Heap
• In operating systems for load balancing and interrupt handling

Advantages #

• Quick access to the top element - O(1)
• Efficient Insertion and Deletion operations - O(log N)

Disadvantages #

• Not suitable for retrieving random elements - O(N)
• Slower than arrays and linked lists for non-priority queue operations

Implementation #

Resources #

• 📝 6.11 Binary Heap Implementation
• 🎓 Algorithms, Part I - Priority Queues